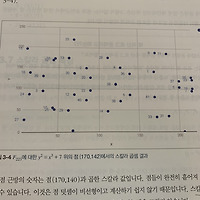
 타원곡선 위 점의 스칼라 곱셈
타원곡선위 한점을 계속 더하는것이다. 그리고 그 결과는 예측하기 어렵다. $ (170,142) + (170, 142) = 2 \cdot (170, 142) $ $ 2 \cdot (170, 142) + (170, 142) = 3 \cdot (170, 142) $ prime = 223 a = FieldElement(0, prime) b = FieldElement(7, prime) x1 = FieldElement(170, prime) y1 = FieldElement(142, prime) p = Point(x1, y1, a, b) print(p + p) 스칼라 곱셈의 또다른 특징이 있다. 어떤 점에 스칼라 값을 계속 증가시키면서 곱하다 보면 무한원점(덧셈에 대한 항등원. I) 에 도달한다. 그래서 만약 어떤 점..
2022. 10. 29.
타원곡선 위 점의 스칼라 곱셈
타원곡선위 한점을 계속 더하는것이다. 그리고 그 결과는 예측하기 어렵다. $ (170,142) + (170, 142) = 2 \cdot (170, 142) $ $ 2 \cdot (170, 142) + (170, 142) = 3 \cdot (170, 142) $ prime = 223 a = FieldElement(0, prime) b = FieldElement(7, prime) x1 = FieldElement(170, prime) y1 = FieldElement(142, prime) p = Point(x1, y1, a, b) print(p + p) 스칼라 곱셈의 또다른 특징이 있다. 어떤 점에 스칼라 값을 계속 증가시키면서 곱하다 보면 무한원점(덧셈에 대한 항등원. I) 에 도달한다. 그래서 만약 어떤 점..
2022. 10. 29.
 타원곡선 덧셈
타원곡선 위의 점 덧셈 기본원리는 아래 그림과 같다. 덧셈에 대한 모든 케이스는 아래 세가지로 나눠서 따져봐야한다. 1. 두 점이 x 축에 수직인 직선 위에 있는 경우 p1 = Point(-1, -1, 5, 7) p2 = Point(-1, 1, 5, 7) inf = Point(None, None, 5, 7) print(p1 + inf == p1) print(p2 + inf == p2) print(p1 + p2 == inf) def __add__(self, other): # None 은 무한원점을 의미한다. self 가 무한원점이면, other 를 리턴. ex) A(other) + I(self) = A if self.x is None: return other # other.x 가 무한원점이면, self 를..
2022. 10. 29.
타원곡선 덧셈
타원곡선 위의 점 덧셈 기본원리는 아래 그림과 같다. 덧셈에 대한 모든 케이스는 아래 세가지로 나눠서 따져봐야한다. 1. 두 점이 x 축에 수직인 직선 위에 있는 경우 p1 = Point(-1, -1, 5, 7) p2 = Point(-1, 1, 5, 7) inf = Point(None, None, 5, 7) print(p1 + inf == p1) print(p2 + inf == p2) print(p1 + p2 == inf) def __add__(self, other): # None 은 무한원점을 의미한다. self 가 무한원점이면, other 를 리턴. ex) A(other) + I(self) = A if self.x is None: return other # other.x 가 무한원점이면, self 를..
2022. 10. 29.